Le contexte bio-médical
Le poumon est organisé en une série de bifurcations de bronches à partir de la trachée. Elles deviennent de plus en plus petites jusqu’aux acini, de petits sacs où le sang affleure et où l’oxygène s’y dissout, ce qui nous permet d’alimenter l’ensemble de notre organisme en oxygène. Si on étalait toute la surface de la paroi du poumon en contact avec l’air que nous inhalons, cela représenterait la surface de quatre bus mis côte à côte ! Cette paroi est composée en surface de cellules dites épithéliales qui s’assemblent comme des légos pour former l’épithélium, un tissu formé à la surface des cellules sur laquelle vont pouvoir passer les sécrétions. (voir la figure 1). Certaines de ces cellules sont des cellules caliciformes ou « gobelets » qui produisent des protéines– les mucines – s’agglomérant dans le fluide ambiant pour former le mucus bronchique. Mais la plus grosse partie de l’épithélium respiratoire est composé de cellules ciliées, c’est à dire possédant des cils qui transportent le mucus. Ce mécanisme est très important pour nous, car le mucus piège les bactéries, virus, pollens, poussières, et micro-particules. Ces aérosols remontent ainsi jusqu’à la trachée (on parle de clairance mucociliaire) avant d’être détruits dans l’estomac.

Ainsi le battement ciliaire permet de transporter le mucus vers la gorge (le carrefour pharyngo-laryngé) où il est avalé et détruit dans l’estomac. Il nous protège de tous les aérosols dangereux que nous inhalons au quotidien ! Hélas, certaines pathologies empêchent le battement ciliaire de fonctionner, et dans ce cas le mucus stagne et les bactéries capturées peuvent proliférer, ce qui devient dangereux voire mortel. C’est le cas de la mucoviscidose, la maladie génétique sévère la plus répandue en occident, qui affecte de nombreux organes, et qui altère la protéine CFTR de la membrane pulmonaire. Le rôle de cette dernière est de permettre les échanges entre l’intérieur et l’extérieur des cellules épithéliales – comme un canal – afin de réguler la quantité de liquide à la surface de l’épithélium, et permet ainsi d'hydrater/d'humidifier le mucus [8]. Son dysfonctionnement altère le mucus de protection à l’intérieur des bronches et autorise malheureusement les bactéries à proliférer [1].
Le but du projet MucoReaDy (pour Respiratory Dysfunction), est d’établir un modèle mathématique de ce système epithélium+mucus et de prévoir si un mucus est fonctionnel ou pas : les solutions numériques de ce modèle miment le fonctionnement de ce système biologique et on parle ainsi de jumeau numérique. Les prélèvements de mucus de patients dans les CHUs partenaires de cette étude ont plusieurs objectifs. D’une part ils permettent de vérifier si ce jumeau numérique développé par les chercheurs est satisfaisant, et d’autre part de pouvoir mettre sous monitoring un patient suivant une nouvelle thérapie afin de suivre quantitativement l’état de son mucus, notamment les modulateurs CFTR (dont les trithérapies depuis 2020) qui font refonctionner le canal CFTR [2,10].

La modélisation mathématique de l’épithélium respiratoire
Si on considère le petit volume autour d’une cellule ciliée et du mucus, c’est-à-dire une petite boite de 20 micromètres de côté (soit environ 4 fois plus petit que l’épaisseur d’un cheveu), on peut mettre en équation la vitesse de déplacement du mucus. Cette vitesse est inconnue et on cherche à la déterminer dans cette boîte. C’est une fonction qui dépend du lieu et du moment où on fait l’observation. Autrement dit la vitesse du mucus est décrite par sa vitesse dans les trois dimensions de l’espace dans lequel on vit : largeur, hauteur et profondeur. Ces trois vitesses sont solution d’une équation plus complexe, appelée équation aux dérivées partielles [9]. Ce type d’équation fait intervenir plusieurs autres quantités physiques, telles que la viscosité ou la concentration de mucines, qui sont aussi des fonctions inconnues. Chacune de ces fonctions est d’ailleurs elle-même solution d’une équation particulière.
Arriver à formuler toutes ces équations de types différents est une discipline appelée la modélisation mathématique d’un phénomène physique. Les mathématiciens peuvent s’intéresser à plusieurs aspects. Tout d’abord, garantir que le modèle (la représentation mathématique) a un sens : est-ce que sa solution existe ? Sinon inutile de se casser la tête à le résoudre… Est-elle unique ? On peut ainsi parler de LA solution. Mais aussi trouver si la solution présente des sauts de valeurs (on parle de discontinuités), ou des ruptures de pentes (des changements nets de direction dans la représentation graphique), est-ce qu’on peut globalement la mesurer, ou mesurer ses variations, etc… Cette discipline s’appelle l’analyse fonctionnelle et apporte un cadre rigoureux aux modèles physiques et mécaniques à toutes les échelles et pour beaucoup de phénomènes !
Pourquoi modéliser ?
En dehors de ces considérations théoriques, les mathématiciens cherchent aussi à approcher de très près la solution de la modélisation de notre épithélium [4-7], car pour des problèmes aussi compliqués, impossible la plupart du temps de trouver une solution qui s’exprime à l’aide de fonctions usuelles. C’est ce dernier point qui intéresse les chercheurs dans ce projet : calculer la vitesse au mieux pour pouvoir fournir le débit moyen de mucus vers la trachée et savoir s’ils ont affaire à une configuration pathologique ou pas. Pour cela, ils travaillent avec des géométries simplifiées (en réduisant les détails) ou idéales (en remplaçant la forme réelle par une représentations géométrique parfaite), mais avec les bons ordres de grandeurs et les plus représentatives possibles (voir la figure 1).

Figure 1. Description de la membrane pulmonaire à l’échelle de quelques microns (à gauche) et schéma simplifié d’une cellule épithéliale ciliée à partir d’un découpage d’image microscope (à droite, tiré de [5]).
Dans cette étude, on s’intéresse à la rhéologie du mucus (l’étude de la déformation et de l’écoulement du fluide quand il subit des forces), et notamment à son aspect rhéo-fluidifiant : comment la viscosité du mucus varie en fonction du cisaillement. Le cisaillement, en mécanique des fluides, c’est quand différentes couches d’un liquide (comme l’eau ou l’air) glissent les unes par rapport aux autres. Un peu comme si on faisait glisser doucement une pile de cartes : chaque couche bouge un peu différemment de celle du dessus ou du dessous. L’unité de mesure du cisaillement est le Hertz, en m/s par m, il permet d’exprimer la variation d’une vitesse sur une distance.
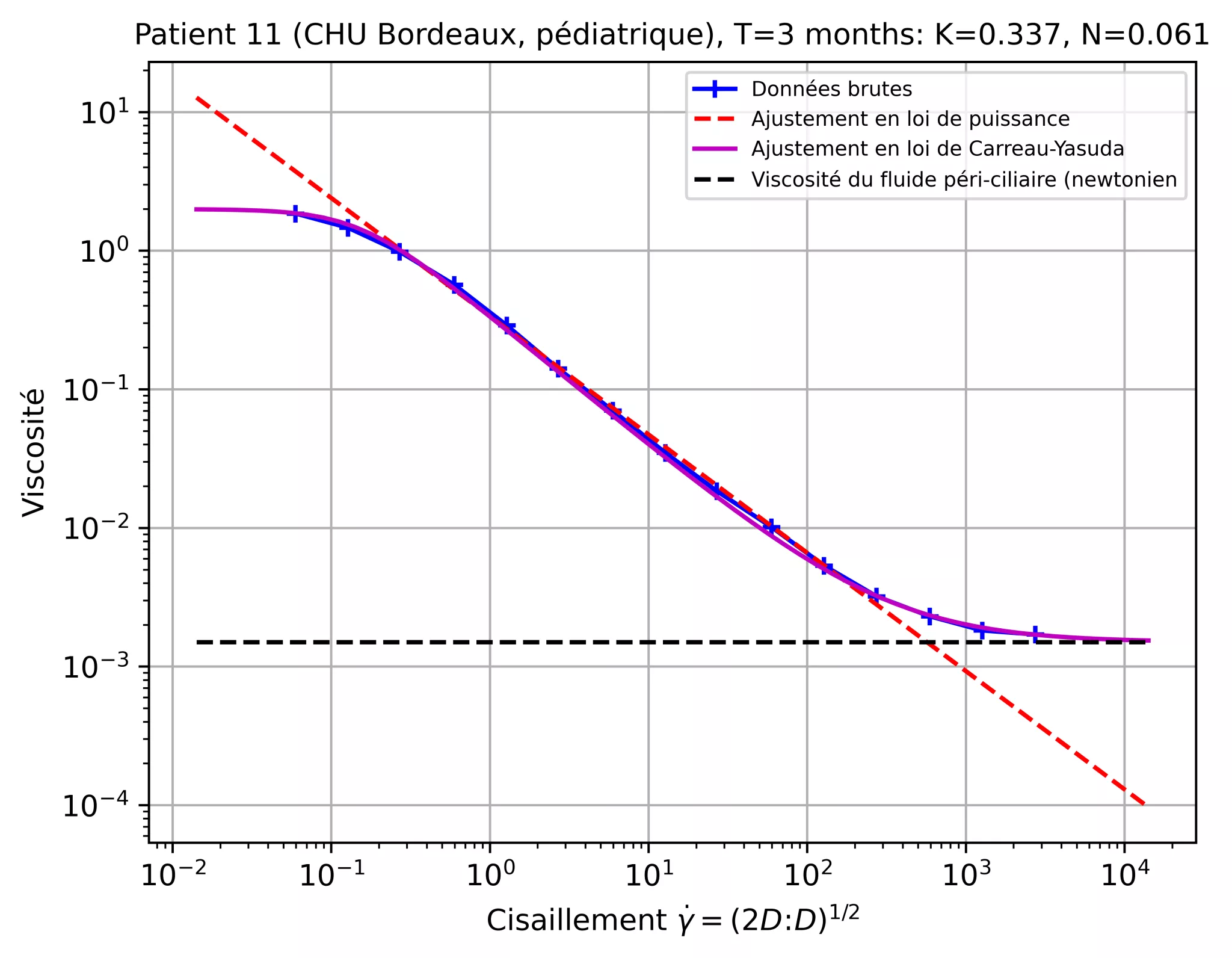
La courbe qui montre la viscosité en fonction du cisaillement est appelée le rhéogramme. Une partie de cette courbe se comporte comme une loi de puissance, autrement dit, elle se comporte comme une droite. Son expression est : viscosité = K x cisaillement N-1. K correspond à la consistance du mucus, tandis que N détermine le changement de viscosité (constant, augmente ou diminue). Les formules des modèles développés par les chercheurs sont un peu plus compliquées (voir la figure 2) car elles comportent plus de paramètres réalistes, comme par exemple la loi de Carreau-Yasuda. Cette dernière permet de décrire le comportement et la viscosité du mucus selon l’augmentation de la vitesse de cisaillement. Sur la figure 2, la droite rouge identifie la partie de la courbe en loi de puissance (une droite en coordonnées logarithmiques) durant laquelle N est constant et correspond à la pente de la droite. L’idée est la suivante : si on est capable de calculer le débit de mucus pour toutes les valeurs de K et N, alors on peut déterminer à l’avance quels sont les couples (K, N) qui sont pathologiques et lesquels sont sains (ou guéris ou contrôlés suivant les pathologies). On obtient alors un diagnostic si on peut évaluer K et N pour un patient. Reste à savoir si ce diagnostic est pertinent, naïf, utilisable, vrai/faux, ou questionnant.
L’analyse des crachats
Le raccord avec l’étude clinique est assez simple dans son principe. Il s’agit tout d’abord d’expliquer le sujet de cette étude à des patients qui débutent une prise en charge dans un CHU (ici Toulouse et Bordeaux) de leur demander leur accord pour récupérer le mucus expectoré lors de leurs séances de kinésithérapie et de drainage respiratoire. Le mucus ainsi recueilli est conservé au froid (-20°C) sur place, au pôle des voies respiratoires au CHU Toulouse, et au Centre de Ressources Biologiques (CRB) au CHU de Bordeaux. Il est alors envoyé par lots à Rhéonova, une entreprise de la banlieue grenobloise spécialisée dans les mesures rhéologiques et la caractérisation des matériaux. Après analyse, ils retournent aux chercheurs les données brutes de rhéologie pour l’ensemble des échantillons qui leur ont été envoyés. Il ne reste alors qu’à déterminer les paramètres correspondant au modèle rhéologique développé par les scientifiques ! La figure 2 montre, pour un prélèvement pédiatrique au CHU de Bordeaux, que la viscosité est une fonction du cisaillement comme cela a été démontré par Yasuda et formalisé dans la loi de Carreau-Yasuda. On constate ici qu’elle est particulièrement bien vérifée, ainsi que la loi de puissance dans la zone intermédiaire du rhéogramme.

Une cartographie du chemin vers la guérison
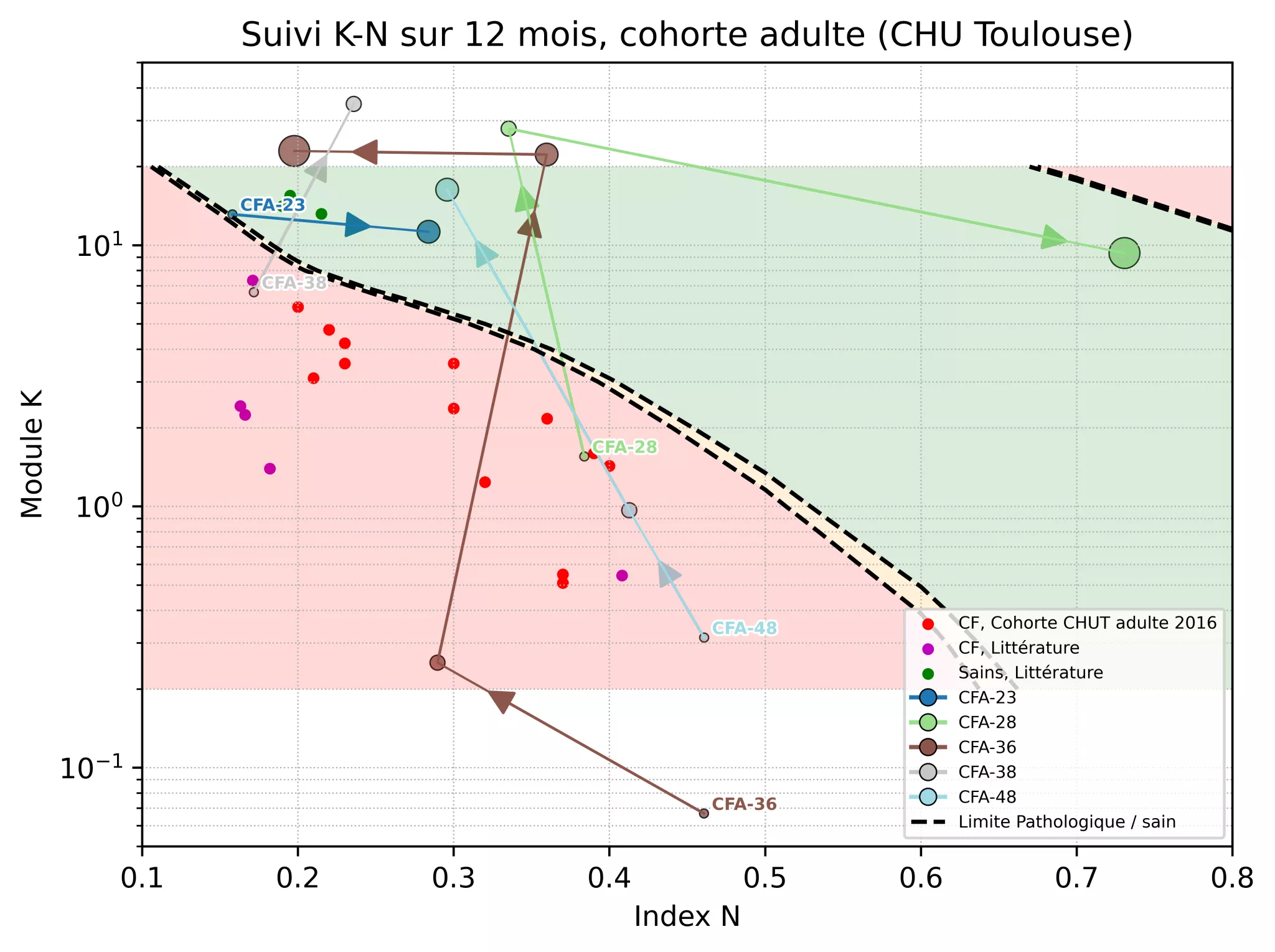
Le calcul permet d’obtenir une cartographie prédictive en fonction des deux paramètres K et N : tout ce qui est en dessous d’une certaine vitesse de mucus est considérée pathologique (en rouge sur la figure 3), et tout ce qui est au-dessus est considéré fonctionnel (sain, en vert sur la figure 3).
Le premier succès obtenu en 2016 fût de porter sur cette carte les couple (K,N) du groupe de patients du CHU de Toulouse[3] et de données bibliographiques (des patients porteurs de mucoviscidose). Ces points rouges et violets sur la figure 3 sont tous dans la région prévue comme pathologique ! Les trois points verts correspondent à des données bibliographiques de 3 personnes saines et confirment également la prédiction d’un mucus fonctionnel.
L’étape suivante, le cœur du projet MucoReaDy, fût de déterminer si cette carte peut servir de suivi lors d’une thérapie. D’autant plus que ce projet a commencé en 2020, début des thérapies de type modulateur de l’activité du canal CFTR (trithérapies) pour la mucoviscidose. Ces thérapies, qui ont plusieurs cibles - dont l’augmentation de la clairance muco-ciliaire, se sont montrées extrêmement efficaces, bien que très chères (de l’ordre de 14000€/mois). Se référer à notre modélisation permet aux médecins de savoir si leurs patients sont répondants à la thérapie (c’est à dire se dirigent vers la zone verte de notre carte). Ce fût le cas pour la totalité les adultes suivis au CHU Toulouse entre 2022 et 2024, et ayant un mucus mesurable (pas sec, pas constitué de salive et sans présence de sang). On voit en effet sur la figure 3 la trajectoire prise : les petits points sont l’état initial d’un patient lors de sa prise en charge au CHU, et les points grossissent en fonction du temps écoulé depuis leur début de prise en charge (les plus gros points représentent 12 mois de traitement). En ce qui concerne la pédiatrie, 70% des enfants de la cohorte suivie au CHU de Bordeaux entre 2023 et 2025 se déplacent vers la zone verte de la carte durant leur traitement par trithérapie.
Cette carte est aussi utile pour les patients porteurs de mutations non éligibles aux trithérapies (pour lesquelles on ne sait pas encore si les trithérapies seront efficaces), ou qui sont non-répondants au traitement (patient en attente d’autres futures thérapies à évaluer). Il est ainsi possible de mesurer la réponse de leur mucus au fil de leur traitement et suivre la direction qu’ils prennent.
Il reste cependant encore beaucoup de travail à faire ! Numériquement, les chercheurs constatent qu’ils doivent explorer plus loin leur domaine (K, N). Ils ont aussi besoin de méthodes numériques toujours plus robustes pour étudier des configurations encore plus raides, c’est-à-dire présentant des variations de plusieurs ordres de grandeurs supérieurs aux configurations étudiées actuellement (des K plus grands, des N plus petits). De plus, le suivi fonctionne sur 100% des adultes testés, mais il s’agit d’une petite cohorte de 9 personnes suivies sur 12 mois. C’est donc un travail préliminaire. Pour 30% des enfants, les résultats ne sont pas explicables et ne répondent à aucun lien avec le sexe, le poids, la taille ou l’âge. Mais l’épithélium pulmonaire des enfants a des caractéristiques différentes des cellules-types utilisées pour nos calculs : il faut à présent caractériser les configurations pédiatriques et faire une étude plus ciblée sur la pédiatrie.
Enfin, on peut remarquer que la guérison est toute relative. La mucoviscidose est une maladie génétique, qui affecte de nombreux organes car la protéine CFTR est présente dans de nombreux tissus, autres que les poumons. Ici, on se focalise uniquement sur l’atteinte respiratoire. La trithérapie tente de réparer fonctionnement du canal CFTR hydratant le mucus, mais les symptômes réapparaissent lorsque le traitement est arrêté (parfois juste car les patients se sentent mieux !). La cartographie permet aussi de savoir où on en est lorsque la prise de traitement est incertaine. Ces données sont expérimentales mais soulignent l'intérêt d'une collaboration entre scientifiques d'horizons différents pour réfléchir à de nouveaux outils d'évaluation plus fins, allant au plus près du mécanisme d'action des nouveaux traitements à l'étude. Ainsi les connaissances sur la mobilité du mucus continueront d’être consolidées dans les années à venir…
Financeur : Financement ANR Interfaces : mathématiques, sciences du numérique, biologie, santé, Projet MucoReaDyANR-20-CE45-0022.

